
Inductive and deductive reasoning are fundamental approaches in critical thinking, reading, and writing. Understanding the differences between them is crucial for constructing and evaluating arguments effectively.
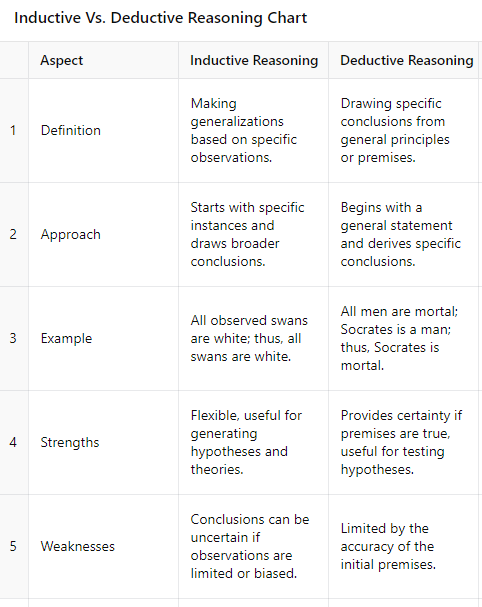
Inductive reasoning involves making generalizations based on specific observations or evidence. It is also known as informal logic. This approach starts with specific instances and draws broader conclusions. For example, observing that "all observed swans are white" may lead to the general conclusion that "all swans are white." Inductive reasoning is often used in scientific research and everyday decision-making, but it can be prone to errors if the observations are limited or biased. This is why inductive reasoning is considered either strong (most likely true) or weak (fallacious).
Deductive reasoning, on the other hand, begins with a general premise or principle and derives specific conclusions from it. It is also known as formal logic. This method is more rigid and structured, ensuring that if the premises are true, the conclusion must also be true. For example, starting with the general statement "all men are mortal" and the specific instance "Socrates is a man," we can deduce that "Socrates is mortal." Deductive reasoning is commonly used in the field of formal logic and mathematics, and its arguments are either valid (necessarily true) or invalid (fallacious).
In critical thinking, both inductive and deductive reasoning are essential. Inductive reasoning allows us to form hypotheses and theories based on observed data, while deductive reasoning helps us test these hypotheses and draw reliable conclusions. By mastering these reasoning techniques, we can enhance our ability to analyze, construct, and evaluate arguments effectively in both academic and everyday contexts.
"Data!data!data!" he cried impatiently. "I can't make bricks without clay.”
― Sir Arthur Conan Doyle, “The Adventure of the Copper Beeches” - a Sherlock Holmes Short Story pg 4 Version 3.1 under Public Domain
Perhaps you have lost a shoe, a homework assignment, the car keys…a mystery to be solved. How do you solve it? How do you find the lost items? How do you solve the mystery? It is elementary, of course, we use our logic. Specifically, we use inductive and deductive reasoning.
One of the most famous solvers of literary mystery is Sherlock Holmes. Perhaps you have heard of him? Holmes is an excellent example of how to put into use inductive and deductive reasoning.
Of course, we don’t have to be solving a mystery to use inductive and deductive reasoning. These forms of logic are used from government leaders to the everyday citizen. As we explore these forms of reasoning, see if you can recognize when you have or are using them!

This diagram summarizes some of the key terminology related to arguments: they can be either deductive, in which the conclusion follows the general premises, or inductive, in which a probable conclusion is reached based on some observed premises. You can determine the validity or the strength of an argument by assuming that the premises are true, then seeing if the conclusion is the expected result.
Inducere, the Latin for induction, means to lead in. It is to reason to a conclusion about a class based on carefully looking at a few members of the class. Thus it looks, usually, from the smaller to the larger. When we use inductive reasoning, we observe, find data, draw inferences about patterns or meanings. We use this kind of reasoning when the sample size is so big we can’t look at everything. How many fish are in the sea? We sample and estimate to find this answer. We use enumeration to do this. Enumeration means to count off one by one or determine the number by counting. Induction uses counting to find statistics. Then we use the result to figure out the most likely conclusion based on controlled sampling of pieces.
This jar of M&Ms has exactly 500 candies.
This second jar of M&Ms has exactly 500 candies.
This third jar of M&Ms has exactly 500 candies.
(Thus) all jars of M&Ms must have exactly 500 candies.
Observe that the conclusion says ‘must’, showing that this conclusion is a guess. It is a probability, estimate or extrapolation. A fourth jar might be opened and contain 450 candies, then you will know that sample size is not large enough and thus you are not able to make an accurate conclusion. Then you need to redo the test–count more samples until you find a more reliable sample size to make a more accurate average.
The sun rose two days ago.
The sun rose yesterday.
The sun rose this morning.
Therefore the sun rises every day.
Although this example uses the same number of samples as the previous one, its conclusion is a scientific fact. This is because the actual sample size is much larger. 365 days per year times 4.5 billion years (or even just 300,000 years that humans have been around to observe it) equals a very, very large sample. The size of the sample and the consistency of the result allow us to reach a stronger conclusion. Compare the following two examples? Which of these inductive arguments is strong, and which one is fallacious? Why?
Chickens lays eggs.
Pigeons lay eggs.
Hummingbirds lay eggs.
Therefore all birds lay eggs.
Most universities and colleges in Utah ban alcohol from campus.
Therefore most universities and colleges in the U.S. ban alcohol from campus.
Keep in mind that conclusions drawn from samplings are just estimations and not 100% accurate. However, they can still help us form decisions. For example, if you have a phone that has a battery life starts to get shorter–perhaps it lasts five minutes less for a month, and then the next month it is ten minutes less, and then the next month it is twenty minutes less and so on, then you can induce that the battery will soon not hold a charge. If your phone also has a cracked screen and the microphone is starting to fail, you can decide if it is time to buy a new phone or fix the phone you have. If the problems continue to increase, it is clear that a new phone is the best investment of your money.
Inductive reasoning may also look at analogies to draw conclusions. An analogy is a comparison between two things that seem different. Many teachers use analogies to help students understand unfamiliar subjects by comparing to something the student may be familiar with. In law, analogical reasoning is used when decisions depend on precedent–something similar that has happened before. In science, this kind of reasoning has resulted in discoveries and inventions. For example, Dr. Dennis Stanford, Archeologist for the Smithsonian Institution, in trying to answer the question: when did humans first arrive in North America, observed that Eskimos were able to build boats and navigate the sea to hunt. He used this observation to form an analogy: if Eskimos could do this, could European populations do this as well? By comparing human behavior, he concluded that indeed Early Americans could have arrived by boat from Europe (and Spain) across Atlantic Ice.
Inductive reasoning can also look at patterns, using observation to find details and forms, compare and contrast those to find a pattern. Eventually, finding a pattern can lead to an inference. All the patterns together would be the evidence, which could be called the parts and the generalization of the parts becomes the whole. In medicine, we call this a diagnosis. A doctor will look at the symptoms of a patient to find patterns. The doctor will determine the diagnosis based on analysis of the patterns.
Yet another form of inductive reasoning is looking at cause. Causal reasoning explains why things occur, continue or vanish. Causal reasoning is very important to survival. We use this often without even thinking about it. Causal reasoning influences many of our behaviors. For example, if I eat this chocolate, I may get diabetes. This is because one cause of diabetes can be eating too much sugar. This may be even more important if we have a family history of diabetes. My family has a high risk for diabetes. I am a member of my family; therefore, I have a high risk for diabetes.. This knowledge can help us induce that we need to be more picky about what we eat. It is important to keep in mind that these conclusions need to be accompanied with facts. If there is not evidence, then the conclusion can be fallacious.
We can also reason with hypothesis. Hypothesis means supposition–a tentative explanation for a conclusion. The hypothesis will be tested to find validity or probability. Reasoning through probability, which is about how many times something will occur vs the total number of actual occurrences. Reasoning through statistics, collecting, organizing and interpreting mathematical data, is also used in induction. In statistics, people are working to make accurate predictions from a sampling of parts. It is important to have a well developed sample. If we don’t, we run the risk of committing the fallacy of false statistics.
All of these are how we use inductive reasoning. Keep in mind, inductive reasoning goes from the small to the larger; it is looking out.
Deductive reasoning is the opposite of inductive reasoning in that it seeks to look in, starting big and moving to smaller. Deducere is the Latin for deduction, which looks at something general to get to the specific. It is known as formal logic because it creates forms that serve as models to show both correct and incorrect reasoning. While induction draws from an accumulation of evidence, deduction reasons by using carefully worded statements about relationships between classes, characteristics and individuals.
In the process of deduction, you begin with some statements, called “premises,” that are assumed to be true, you then determine what else would have to be true if the premises are true. For example, you could begin by assuming that God exists, and is good, and then determine what would logically follow from such an assumption. With this premise, you would look for evidence supporting a belief in God. With deduction, you can provide absolute proof of your conclusions, given that your premises are correct. The premises themselves, however, remain unproven and unprovable.
Let's look at a classic example.
All human beings are mortal (class)
Socrates is human (characteristic)
Socrates is mortal (individual)
This kind of reasoning exercise is called a syllogism. We use syllogisms to help us determine if the argument is valid. An argument has a premise– a claim– that must be supported with facts–or evidence–and this evidence must be analyzed–how is it helping prove the claim. So, we can use a syllogism to test the validity of our argument. First we need to determine if the premises are true and second we determine if the syllogism is valid. If both of these are true, then we have a sound argument. If we grant the premise, we must also grant the conclusion. If we grant the premise and not the conclusion, then we are contradictory, making the argument invalid. A sound argument passes the test of content–premises are true as a matter of fact; it passes the test of form–the premise and conclusion are so related that it is not possible for the premise to be true and the conclusion false. Conversely, an unsound argument does not prove its conclusion and suffers from one or both of two failures–not all premises are true, and the argument is invalid.
All fathers are males. (class)
Juan is a father. (characteristic)
Juan is male. (individual)
Juan is a member of the class of father, and all members of that class are males, it follows logically that Juan must be a male. But watch what happens when you swap the second two lines.
All fathers are males. (class)
Juan is a male. (individual)
Juan is a father. (characteristic)
The second version is clearly invalid. he error here is that while all fathers are male, not all males are fathers. Just because Juan belongs to the larger class does not necessitate that he participate in the sub-class.
The rule for determining soundness is that if the premises are both true and the argument is valid, the conclusion can’t be false. In order to determine this, we ask: Is the argument vulnerable to criticism on the grounds that one or more of its premises are false? Or are the inferences themselves an issue because even if all premises are true, the conclusion still won’t follow? These are the questions we will consider when determining the validity of an argument.
We can use syllogisms to find if an argument is valid and we can use them to find hidden assumptions.
The burritos at Julio’s are Grandisimos
As a syllogism it reads:
Grandisimo (big) burritos are better (hidden assumption)
Julio's burritos are the biggest
Julio’s Burritos are better (hidden conclusion)
We should buy Julio’s burritos. (Implied conclusion)
(excerpted from Thinking for Yourself 9th edition)
Suspects who are innocent of a crime should be able to have a lawyer present before police questioning. But the thing is you don’t have many suspects who are innocent of a crime…If a person is innocent of a crime, then he is not a suspect.
Here is a translation of this statement into a syllogism:
All innocents are not suspects.
You are a suspect.
You are not innocent.
When you translate the claim, it becomes clear what is wrong with its assertion. The argument is not sound, because the major premise is not true. (341)
Inductive and deductive thinking are not wholly separable. They are often intertwined and they are used daily. We can use them to ensure we won’t be killed; we can use them to find our lost keys or solve the world's greatest mysteries! And as you may have come to suspect, compelling arguments rely on using both. Deduction and induction by themselves are inadequate on their own. While deduction gives absolute proof, it never makes contact with the real world, there is no place for observation or experimentation, and no way to test the validity of the premises. And, while induction is driven by observation, it never approaches actual proof of a theory. Therefore an effective paper will include both types of logic.

Figure: Deductive reasoning starts with an understanding of a general principle, then special cases help support that principle. Inductive reasoning works the other way around, where a special case is observed first, which leads to the eventual understanding of a general principle.
Imagine you are a community college student living in a the Central Valley in an agricultural community. You notice that in the past five years, every summer, the water levels in the local reservoir have dropped significantly. Based on these specific observations, you might induce that the region is experiencing a trend of drier summers.
This inductive reasoning is based on specific data points collected over a period and leads to a broader conclusion about climate trends in the area. However, this conclusion might not be entirely accurate if the observations are not representative of long-term trends or other influencing factors.
Now, consider a scenario where a local farming association publishes a guideline stating, "All farms in the Central Valley that use drip irrigation systems save water compared to those using traditional irrigation methods." You apply this general principle to a specific case on your family's farm.
In this deductive reasoning example, the conclusion logically follows from the premises. If the general statement is true and the specific instance fits the criteria, then the conclusion must be true.
Inductive and deductive reasoning are not just theoretical concepts; they are practical tools used in everyday decision-making. For instance, if you notice that your crops have consistently yielded less during dry years (inductive reasoning), you might decide to invest in drought-resistant crops or advanced irrigation systems. Conversely, if you start with the principle that "drought-resistant crops perform well in dry conditions" (deductive reasoning), you might decide to plant these crops during an expected dry season.
By understanding and applying both inductive and deductive reasoning, you can make more informed and logical decisions, whether you're managing a farm, studying for an exam, or engaging in community debates about resource management. These reasoning skills help you analyze situations, construct valid arguments, and evaluate the claims and evidence presented by others, enhancing your overall critical thinking abilities.
Understanding inductive and deductive reasoning, along with the ability to identify fallacies, is crucial for developing strong critical thinking, reading, and writing skills, particularly in the realm of argumentative reading and writing. Deductive reasoning involves starting with a general principle and reaching a specific conclusion, ensuring that if the premises are true, the conclusion must also be true. Inductive reasoning, on the other hand, involves drawing general conclusions from specific observations, which means that while the conclusions are probable, they are not guaranteed.
Recognizing logical fallacies is equally important. Fallacies are errors in reasoning that can undermine the validity of an argument. Common fallacies include ad hominem attacks, straw man arguments, false dilemmas, and appeals to emotion, among others. These fallacies can distort the truth and mislead audiences, which is why critical thinkers and effective writers must be vigilant in identifying and avoiding them.
In today's media landscape, the ability to apply these reasoning skills is more important than ever. Consider the ongoing discussions around climate change. Deductive reasoning might be used to argue that because scientific principles and data show increased greenhouse gases lead to global warming, the current rise in global temperatures is due to human activity. Inductive reasoning can be seen in how scientists gather data from various climate studies to form broader conclusions about climate trends.
However, the debate is often clouded by fallacies. For example, some arguments against climate change use ad hominem attacks on scientists or present false dilemmas, suggesting that we must choose between economic growth and environmental protection. By applying inductive and deductive reasoning and being aware of fallacies, individuals can better navigate these complex discussions, making informed decisions based on sound logic and evidence.
By integrating these concepts into your argumentative reading and writing, you can critically analyze arguments and construct well-reasoned, persuasive essays. Recognizing fallacies in others' arguments allows you to critique their validity effectively, while avoiding these pitfalls in your writing strengthens your position. Using inductive and deductive reasoning enhances your ability to draw and defend logical conclusions.
In summary, mastering inductive and deductive reasoning, coupled with the ability to identify fallacies, equips individuals to analyze arguments critically and construct well-reasoned, persuasive arguments. These skills are invaluable not only in academic settings but also in everyday life, where clear and logical thinking is essential for informed decision-making. By honing these abilities, you will be better prepared to engage in thoughtful, impactful discourse both inside and outside the classroom.

The content above was assisted by ChatGPT in outlining and organizing information. The final material was curated, edited, authored, and arranged through human creativity, originality, and subject expertise of the Coalinga College English Department and the Coalinga College Library Learning Resource Center and is therefore under the CC BY NC license when applicable. To see resources on AI and copyright please see the United States Copyright Office 2023 Statement and the following case study on using AI assistance but curating and creating with human originality and creativity.
Images without specific attribution were generated with the assistance of ChatGPT 2024 and are not subject to any copyright restrictions, in accordance with the United States Copyright Office 2023 Statement.
All original source content used to remix above came from the following open educational resources:
9.7: Inductive and Deductive Reasoning is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Lumen Learning via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
CC licensed content, Original
Public domain content
3.3: Inductive and Deductive Reasoning is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts.