New models for symbolic data analysis

This approach is potentially extremely attractive given present technological trends requiring the analysis of increasingly large and complex datasets. SDA effectively states that for many analyses, the high level of computation required for e.g. divide-and-recombine techniques (e.g. Guha et al. 2012; Jordan et al. 2019; Vono et al. 2019; Rendell et al. 2020) or subsampling-based techniques (Quiroz et al. 2018; Bardenet et al. 2014; Quiroz et al. 2019), is not necessary to make inference at the group level.

By aggregating the individual-level data to a much smaller number of group level symbols m (where \(m\ll n\) ), ‘big data’ analyses can be performed cheaply and effectively on low-end computing devices. Recent work by Whitaker et al. (2021) has shown that SDA can outperform bespoke subsampling techniques for logistic regression models, in terms of much lower computational overheads for the same predictive accuracy. Beyond data aggregation, distributional-valued observations can arise naturally through the data recording process, representing underlying variability. This can include e.g. observational rounding or truncation, which results in imprecise data known to lie within some interval (Heitjan and Rubin 1991; Vardeman and Lee 2005), and the elicitation of distributions from experts thought to contain quantities of interest (Fisher et al. 2015; Lin et al. 2022). In this sense, Schweizer (1984)’s often-quoted statement that “distributions are the numbers of the future” seems remarkably prescient.

Many SDA techniques for analysing distributional-valued random variables have been developed (and here we take ‘distributional-valued’ random variables to include random intervals or random rectangles that have no specific distributional form aside from the specified quantiles). These include regression models (Irpino and Verde 2015; Le-Rademacher and Billard 2013), time series (Lin and González-Rivera 2016), clustering and classification (Whitaker et al. 2021), discriminant analysis (Duarte Silva and Brito 2015) and Bayesian hierarchical modelling (Lin et al. 2022). Likelihood-based inference was introduced by Le-Rademacher and Billard (2011) and Brito and Duarte Silva (2012) with further development and application by Zhang et al. (2020), Rahman et al. (2022), Lin et al. (2022).

While there have been many successes in the analysis of symbolic data, from a statistical perspective there are many opportunities for methodological improvement. Some of these opportunities relate to existing SDA approaches, under which the statistical unit of interest is the symbol, and where inference is required at this level (either exploratory or statistical inference). For example, the large majority of SDA techniques are descriptive and do not permit statistical inference on model parameters. E.g., regression models tend to be fitted by symbolic variants of least squares. Other opportunities arise, as with the present work, by re-imagining how the ideas behind SDA can be used to solve modern statistical challenges. Here we assume that, as with a standard statistical analysis, inference is required at the level of the individual-level data, but where we deliberately aggregate the individual-level data into symbols prior to the analysis. Hence, if we can develop a way to perform statistical inference on the individual-level data when only given the group-level summaries, then we can potentially perform standard statistical inference for large and complex datasets more efficiently via these distributional summaries than when directly using the original data. This alternative perspective on the ideas underlying SDA methodology opens up a new research direction in the field of SDA. Here, we focus on likelihood-based inference.

The likelihood approach of Le-Rademacher and Billard (2011), Brito and Duarte Silva (2012) maps each symbol to a random vector that uniquely defines the symbol, and then models this via a standard likelihood model. E.g., suppose that \(X_\in <\mathbb >\) is the value of some process recorded on the i-th second, \(i=1,\ldots ,n=86400\) , of the j-th day, \(j=1,\ldots ,m\) . If interest is in modelling these data as, say, i.i.d draws from a skew-normal distribution \(X_\sim SN(\mu _0,\sigma _0,\alpha _0)\) , the likelihood function \(L(x|\theta )\) , \(\theta \in \varTheta \) , may then be easily constructed. However, suppose that interval symbols are now constructed so that \(S_j=(\min _i X_, \max _i X_)\subseteq <\mathbb >\) is the random interval describing the observed process range on day j. Due to the equivalence of representing continuous subsets of \(<\mathbb >\) by the associated bivariate vector in this setting (Zhang et al. 2020), the approach of Le-Rademacher and Billard (2011), Brito and Duarte Silva (2012) constructs a model for the vectorised symbols \(S_1,\ldots ,S_m\) , perhaps after a reparameterisation. For example,

$$\begin S_j\sim SN_2(\mu ,\varSigma ,\alpha )\qquad \text< or >\qquad >_j\sim SN_2(\mu ,\varSigma ,\alpha ), \end$$

where \(>_j=((a+b)/2,\log (b-a))\) is a typical reparameterisation of \(S_j=(a,b)\) into a function of interval mid-point and log range (Brito and Duarte Silva 2012). While there is inferential value in models of these kind (e.g. Brito and Duarte Silva 2012; Lin et al. 2022), it is clear that if there is interest in modelling the underlying \(X_\) as skew-normal, it is difficult to construct even a loosely equivalent model at the level of the symbol \(S_j\) (or \(>_j)\) . That is, while the analyst may intuitively construct complex statistical models at the level of the individual-level data, it is less obvious how to construct models at the symbolic level and for different symbolic forms.

By design, modelling symbols directly, without specifying a probabilistic model for the underlying micro-data, only permits inference and predictions at the symbol level. This is unsatisfactory because predictive inference for the underlying micro-data is often of interest, even if primary focus is on group-level analysis, and as we demonstrate in Sect. 3.3, ignoring the structure of the micro-data can result in symbolic-level analyses producing poorer inferential outcomes. Another clear and acknowledged problem (Kosmelj et al. 2014; Cariou and Billard 2015) is that even though existing SDA techniques do not focus on the individual-level data, the distribution of this data within random intervals/rectangles and within histogram bins is typically assumed to be uniform. Alternatives include the triangular distribution (Le-Rademacher and Billard 2011; Dias and Brito 2017). When considering that random intervals are typically constructed by specifying \(S_j=(\min _i X_, \max _i X_)\) , it is almost certain that the distribution of the underlying data within \(S_j\) is non-uniform. This implies that any inferential procedure built on the uniformity assumption (i.e. almost all current SDA methods) is likely to produce questionable results.

One principled difference between SDA and regular statistical analyses is that the analysed symbolic data can be constructed by the analyst. This raises the question of how this should be undertaken. Intuitively, if looking to design, say, a random interval \(S_j\) to maximise information about a location parameter, using the sample maximum and minimum is likely a poor choice as these statistics are highly variable. A more useful alternative could use e.g. sample quantiles to define the interval. While sample quantiles have been considered in SDA methods, they have only been used as a robust method to avoid outliers that would otherwise dominate the size of a random interval (Hron et al. 2017). In general, little consideration has been given to the design of informative symbols.

In this paper we introduce a novel general method for constructing likelihood functions for symbolic data based on specifying a standard statistical model \(L(X|\theta )\) for the underlying measurement-level data and then deriving the implied model \(L(S|\theta )\) at the symbolic level by considering how S is constructed from x. This construction assumes that we are in the setting where the symbolic data are created through a data aggregation process. This provides a way to fit the measurement-level data model \(L(X|\theta )\) while only observing the symbol level data, S. It provides both a natural way of specifying models for symbolic data, while also opening up SDA methods as a mainstream technique for the fast analysis of large and complex datasets. This approach naturally avoids making the likely invalid assumption of within-symbol uniformity, allows inference and predictions at both the measurement data and symbolic data levels, permits symbolic inference using multivariate symbols (a majority of symbolic analyses are based on vectors of univariate symbols), and can provide a higher quality of inference than standard SDA techniques. The method recovers some known models in the statistical literature, as well as introducing several new ones, and reduces to standard likelihood-based inference for the measurement-level data (so that \(L(S|\theta )\rightarrow L(X|\theta )\) ) when \(S\rightarrow X\) .

As a result we demonstrate some weaknesses of current symbol construction techniques. In particular we establish informational limits on random rectangles constructed from marginal minima/maxima or quantiles, and introduce a new class of quantile-based random rectangles. These alternative symbol variations produce more efficient analyses than existing symbol constructions, and permit the estimation of within-symbol multivariate dependencies that were not previously estimable.

The new symbolic likelihood function is presented in Sect. 2 with specific results for random rectangles and histograms. All derivations are relegated to the Appendix. The performance of these models is demonstrated in Sect. 3 through a meta-analysis of univariate histograms, a simulation study of the inferential performance of an alternative class of multivariate random rectangle constructions, and an analysis of a large loan dataset. In all cases, the existing state-of-the-art models and symbolic constructions are outperformed by the new symbolic model. Section 4 concludes with a discussion.

Throughout this manuscript we adopt the convention that upper case letters X denote (vector or scalar) random variables, whereas lower case letters x denote their observed values. We also write matrices (as vectors of random variables) \(>, >\) in bold font.

2 A general construction tool for symbolic likelihoods

2.1 Symbolic likelihood functions

Consider that \(\varOmega \) is a sample space defined on a probability space \((\varOmega , <\mathcal >, <\mathbb P>)\) , and that each element of \(\varOmega \) is described by a measurable random variable X, defined by \(X: \varOmega \rightarrow <\mathcal >,\) and \(<\mathbb P>(X \in <\mathcal >) = <\mathbb P>( \omega \in \varOmega | X(\omega ) \in <\mathcal >), \text < for ><\mathcal >\subset <\mathcal >.\) We follow the standard SDA construction of a class (Billard and Diday 2003) and let the random variable \(C: \varOmega \rightarrow <\mathcal >\) denote the class to which an individual belongs. For simplicity we assume that \(<\mathcal >= \< 1, \ldots , m\>\) is finite. Consequently let \(\varOmega _c = \< \omega \in \varOmega \text < s.t.>~C(\omega ) =c \> \subseteq \varOmega \) be the set of all possible outcomes that belong to class \(c \in <\mathcal >\) , and define \(X_c: \varOmega _c \rightarrow <\mathcal >_c \subseteq <\mathcal >\) as the random variable that describes them. No assumptions about the countability of \(\varOmega \) or \(\varOmega _c\) are made since the results presented in this manuscript hold for both discrete and continuous random variables. We assume that we have a population of size N for which the variables \(X_1, \ldots , X_N\) are measured and given in vector form by \(>= (X_1, \ldots , X_N)\) . The population is itself decomposed into m sub-populations of size \(N_c\) such that \(\sum _>> N_c = N\) , corresponding to the groups of individuals belonging to class c. For each class \(c \in <\mathcal >\) , we define by \(>_c = (X_, \ldots , X_ )\) the vector of random variables describing the population of class c.

We now consider an interpretation of SDA, where the symbolic random variable \(S_c\) for class \(c \in <\mathcal >\) is assumed to be the result of the aggregation of the random vector \(>_c \) via some aggregation function \(\pi _c\) , so that \(S_c = \pi _c (>_c): [<\mathcal >_c]^ \rightarrow <\mathcal >_c\) and \(>_c \mapsto \pi (>_c).\) That is, a symbolic random variable is a statistic which represents a summary of the information brought by measurement over individuals. The choice of this summary (and thus of the aggregation function) is critical and we explore this in later sections. In the following we refer to random variables of the measurement-level data X as classical random variables. By construction symbolic random variables require knowledge of the underlying classical random variables. Accordingly, this should also be true when dealing with likelihood functions, particularly if inference is required at both classical and symbolic levels, but when only information at the symbolic level is observed.

To construct a symbolic likelihood function, suppose that the classical random variable X has probability density and distribution functions \(g_X (\,\cdot \,; \theta )\) and \(G_X (\,\cdot \,; \theta )\) respectively, where \(\theta \in \varTheta \) . Consider a random classical data sample \(>= (x_1, \ldots , x_n)\) of size \(n_c = (x_, \ldots , x_)\) , the collection of those in class c, where \(\sum _>> n_c = n\) . Similarly let \(s_c = \pi _c (>_c)\) be the resulting observed symbol obtained through the aggregate function \(\pi _c\) and define the symbolic dataset to be the collection of symbols \( >= (s_c; c \in <\mathcal >)\) .

Proposition 1

For the subset \(>_c\) of \(>\) associated with class \(c \in <\mathcal >\) , the likelihood function of the corresponding symbolic observation \(s_c=\pi _c(>_c)\) is given by

where \(>_c \in <\mathcal >_c^\) is a subset of \(>\in <\mathcal >^n\) , \(f_>_c>(\cdot ; \vartheta )\) is the conditional density of \(S_c\) given \(>_c\) and \( g_<>>(\,\cdot \,; \theta )\) is the joint density of \(>\) .

We refer to \(L(s_c; \vartheta , \theta )\) given in (1) as the symbolic likelihood function. A discrete version of (1) is easily constructed. Note that by writing the joint density \(g_>>(\,\cdot \,; \theta )=g_>_c>(\,\cdot \,; \theta ) g_>_| >_c>(\,\cdot \,; \theta )\) , where \(>_ = >\backslash >_c\) , then after integration with respect to \(>_ = >\backslash >_c\) , equation (1) becomes

This construction method can easily be interpreted: the probability of observing a symbol \(s_c\) is equal to the probability of generating a classical dataset under the classical data model that produces the observed symbol under the aggregation function \(\pi _c\) . That is, we have established a direct link between the user-specified classical likelihood function \(L(>|\theta )\propto g_>(>;\theta )\) and the resulting probabilistic model on the derived symbolic data. As a result we may directly estimate the parameters \(\theta \) of the underlying classical data model, based only on observing the symbols \(>\) .

In the case where there is no aggregation of \(>_c\) into a symbol, so that \(\pi (>_c)=>_c\) and \(<\mathcal >_c = [<\mathcal >_c]^\) , then \( f_>_c = >_c> (s_c) \equiv f_<\pi (>_c) | >_c = >_c> (\pi (>_c)) = f_<>_c | >_c = >_c> (>_c) = \delta _<>_c> (>_c)\) , where \(\delta _<>_c> (>_c)\) is the Dirac delta function, taking the value 1 if \(>_c = >_c\) and 0 otherwise. As a result the symbolic likelihood function reduces to \(g_<>_c>( >_c; \theta )\) , the classical likelihood contribution of class c. Under the assumption that the classical data are independently distributed between classes, so that \(g_>(\,\cdot \,; \theta ) = \prod _>> g_<>_c>(\,\cdot \,; \theta )\) , the associated symbols are also independent and the likelihood of the symbolic dataset \(>\) is given by

If, further, the observations within a class \(c \in <\mathcal >\) are independent and identically distributed, then in the scenario where \(\pi (>_c) = >_c\) we have \( L(\theta ) = \prod _^n g_X (x_i; \theta ). \) Because \(\text (<\mathcal >) = m\) and typically \(m\ll n\) , this implies that large computational savings can be made through the analysis of symbolic rather than classical data, depending on the complexity of the classical data likelihood function. The method established in Proposition 1 specifies a probability model for the micro-data which, combined with knowledge of the aggregation process \(\pi \) , induces a likelihood function at the aggregate level. In contrast, the likelihood function defined by Le-Rademacher and Billard (2011), Brito and Duarte Silva (2012) specifies a probability model directly on the symbols.

While we do not pursue this further here, we note that the function \(f_>_c>(\cdot ; \vartheta )\) is not constrained to be constructed from Dirac functions (such as when \(S_c\) is fully determined by \(>_c\) ), and may be a full probability function. This allows for the incorporation of randomness in construction of the symbols from the micro-data, such as the random allocation of the micro-data to different symbols. The parameters \(\vartheta \) are fixed quantities that determine the structure of how a symbol will be constructed, e.g., the locations of bins for histogram symbols. While we explore this in Sect. 3 where we introduce a number of new ideas in symbol construction techniques, there is much scope, beyond this paper, to explore these ideas further.

In the following subsections, we establish analytical expressions of the symbolic likelihood function based on various choices of the aggregation function \(\pi \) , which leads to different symbol types. The performance of each of these models will be examined in Sect. 3. For clarity of presentation the class index c is omitted in the remainder of this section as the results presented are class specific.

2.2 Modelling random intervals

The univariate random interval is the most common symbolic form, and is typically constructed as the range of the underlying classical data e.g. \(S=(\min _i X_i, \max _i X_i)\) . Here we generalise this to order statistics \(S=(X_,X_)\) for indices \(l\le u\) given their higher information content. We define an interval-valued symbolic random variable to be constructed by the aggregation function \(\pi \) where

$$\begin S = \pi (>): <\mathbb R>^ \rightarrow <\mathcal >= \< (a_1, a_2) \in <\mathbb R>^2: a_1 \le a_2 \> \times <\mathbb > \end$$

so that \(>\mapsto (x_, x_, N)\) , where \(x_\) is the k-th order statistic of \(>\) and \(l,u \in \< 1, \ldots , N \>, l \le u\) are fixed. Taking \(l=1, u=N\) corresponds to determining the range of the data. (Note that modelling an interval \((a_1,a_2)\in <\mathbb >^2\) as a bivariate random vector is mathematically equivalent to modelling it as a subset of the real line \((a_1,a_2)\subseteq \) . See e.g. Zhang et al. 2020). Note that this construction explicitly includes the number of underlying datapoints N in the interval as part of the symbol, in direct contrast to almost all existing SDA techniques. This allows random intervals constructed using different numbers of underlying classical datapoints to contribute to the likelihood function in relation to the size of the data that they represent. This is not available in the construction of Le-Rademacher and Billard (2011), Brito and Duarte Silva (2012).

Lemma 1

Consider a univariate interval-valued random variable \(S = (s_l, s_u, n) \in <\mathcal >\) , obtained through (2) and assume that \(g_>(>; \theta ) = \prod _^n g_X(x_i; \theta ), >\in <\mathbb R>^n\) , where \(g_X\) is a continuous density function with unbounded support. The corresponding symbolic likelihood function is then given by

It is worth noting that this expression can also be obtained by evaluating \(<\mathbb P>(S_l \le s_l, S_u \le s_u) = <\mathbb P>( X_ \le s_l, X_ \le s_u )\) and then taking derivatives with respect to \(s_l\) and \(s_u\) , and corresponds to the joint distribution of order two statistics. This model was previously established by Zhang et al. (2020) as a generative model for random intervals built from i.i.d. random variables.

2.3 Modelling random rectangles

The typical method of constructing multivariate random rectangles from underlying d-dimensional data \(X \in <\mathbb R>^d, d \in <\mathbb >\) is by taking the cross product of each d univariate random interval described by their marginal minima and maxima (e.g. Neto et al. 2011; Ichino 2011). The number of datapoints underlying this rectangle is often not used. We improve on this scheme by making use of additional information available at the time of rectangle construction (Sect. 2.3.1), and then develop several alternative constructions for random rectangles based on marginal order statistics (Sect. 2.3.2).

2.3.1 Using marginal maxima and minima

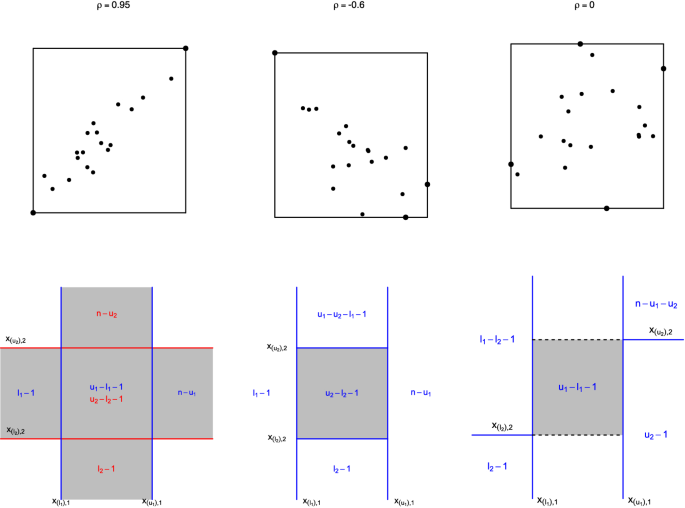
While it is in principle possible to identify a small amount of information about the dependence between two variables summarised by a marginally constructed bounding box, this information content is very weak, and the direction of dependence is not identifiable (Zhang et al. 2020). E.g. if n datapoints are generated from a multivariate distribution and the marginal minimum and maximum values recorded, what can be said about the correlation strength and direction? We propose that dependence information can be obtained if the locations of those datapoints involved in construction of the bounding rectangle, and the total number of points are known. For the examples in Fig. 1 (top), if the rectangle is generated from only two points (left panel) one can surmise stronger dependence than if three points are used (centre), with rectangle construction using four points (right) producing the weakest dependence. The exact locations of these bounding points is informative of dependence direction. (We note that the data points used to construct a multivariate random rectangle are immediately obtained when constructing the random rectangle in the usual way.)

As such, we define the aggregation function \(\pi \) to incorporate these construction points (where available) into the definition of the random rectangle as

so that \(>\mapsto \left( (x_, x_)_, p, I(p), N \right) ,\) where \(>= (x_1, \ldots , x_n)\) , \(x_j = (x_, \ldots , x_)^\top \) and \(x_\) is the k-th order statistic of the i-th marginal component of \(>\) . The quantity p represents the number of unique points involved in constructing the rectangle. The quantity I(p) contains those points that reside in any marginal vertex (in 2 dimensions or higher) in the d-dimensional rectangle. (A ‘marginal vertex’ is a vertex of a lower dimensional marginal rectangle.) In this context a symbol is written as \(S = (S_<\min >, S_<\max >, S_p, S_, N)\) , where \(S_<\min >\) and \(S_<\max >\) are respectively the d-vectors corresponding to the marginal minima and maxima.

Lemma 2

Consider a multivariate random rectangle \(S \in <\mathcal >\) , obtained through (3) and assume that \(g_>(>; \theta ) = \prod _^n g_X(x_i; \theta ), >\in <\mathbb R>^\) , where \(g_X\) is a continuous density function with unbounded support. Then the symbolic likelihood function is given by

$$\begin L(s; \theta ) = \frac \left[ \int _>^> g_X(z; \theta ) <\mathrm >z \right] ^ \times \ell _, \end$$

where the multivariate integral is taken over the rectangular region defined by \(s_<\min >\) and \(s_<\max >\) , and where \(\ell _\) is defined as follows. If \(s_p=2\) then \(s_=(s_a,s_b)\) is the two co-ordinates of d-dimensional space which define the bounding rectangle, and \(\ell _2 = g_X(s_a; \theta ) g_X(s_b; \theta )\) . If \(s_p=2d\) then \(s_ = \emptyset \) and

where \(X_i\) is the i-th component of X, \(X_ = X \backslash X_i\) and similarly for \(s_<\min , -i>,\) \(s_<\max , -i>,\) \(s_<\min , i>\) and \(s_<\max , i>\) , and \(G_ \) is the conditional distribution function of \(X_\) given \(X_i\) .

In (5) the product terms represent the joint distributions of \(X_\) being between \(s_<\min , -i>\) and \(s_<\max , -i>\) given that \(X_i\) is equal to \(s_<\min , i>\) or \(s_<\max , i>\) . When \(s_p=2\) , (5) reduces to \(\ell _=\ell _2\) . General expressions for \(\ell _\) for \(p\ne 2\) or 2d can be complex. Simple expressions are available for \(s_p=3\) when \(d=2\) .

Corollary 1

For a bivariate random rectangle, if \(s_p=3\) then \(S_ = s_c \in <\mathbb R>^2\) is the co-ordinate of the point defining the bottom-left, top-left, top-right or bottom-right corner of the rectangle.

In this case, if \(>_c\) is the element-wise complement of \(s_c\) , i.e. \(>_ = \, s_<\max ,i>\> \backslash \, i=1,2\) , then

E.g. if \(s_c = (s_<\min ,1>, s_<\min ,2>)\) is in the bottom-left corner, then \(>_c = (s_<\max ,1>, s_<\max ,2>)\) .

The first term in (6) is the density of the point in the corner of the rectangle, and the other terms are the probabilities of the two points on the edges being between two interval values given that the other component is fixed. Qualitatively similar expressions can be derived for d-dimensional random rectangles in the cases where \(s_p\ne 2\) or 2d, although there is no simple general expression.

2.3.2 Using marginal order statistics

$$\begin S = \pi (>): <\mathbb R>^\rightarrow & <> <\mathcal >= \< (a_1, a_2) \in <\mathbb R>^2: a_1 \le a_2 \>^d \times <\mathbb > \end$$ $$\begin >\mapsto & <> \left( \left( x_, x_ \right) _, N \right) . \end$$

In this context the symbol is written as \(S=(S_l, S_u,N)\) , where \(S_l\) and \(S_u\) are respectively the d-vectors corresponding to the marginal lower and upper order statistics. This process is illustrated in Fig. 1 (bottom left panel) in the \(d=2\) setting. For fixed l and u, the observed counts in each region are then known as a function of the construction (8). The resulting symbolic likelihood function is then

$$\begin L(s; \theta ) = \prod _^d L(s_, s_, n; \theta _i) \end$$

where \(L(s_, s_, n; \theta _i)\) is as obtained in Lemma 1 using the i-th marginal distribution with parameter \(\theta _i\in \varTheta \) . However, as the construction (8) only contains marginal information, such a symbol will fail to adequately capture dependence between variables. As an alternative, we introduce two new order-statistic based representations of random rectangles that do account for such dependence.

The first, sequential nesting (Fig. 1, bottom centre panel), constructs the order statistics within dimension i conditionally on already being within the random rectangle in dimensions \(j $$\begin >\mapsto \left( \left( \left( x_, x_ \right) | \< x_< x_j< x_; j \right) _, N \right) . \end$$

As before, \(S=(S_l,S_u,N)\) , but where the known observed counts now lie in different regions (Fig. 1), and with the additional constraints of \(2 \le u_ \le u_i - l_i - 1\) .

Lemma 3

Consider a multivariate random rectangle \(S \in <\mathcal >\) , constructed via (9) and suppose that \(g_>(>; \theta ) = \prod _^n g_X(x_i; \theta ), >\in <\mathbb R>^ \) , where \(g_X\) is a continuous density function with unbounded support. The symbolic likelihood function is then given by